3 Merge Sort, Quicksort and Divide-and-Conquer Algorithms
Contents
3 Merge Sort, Quicksort and Divide-and-Conquer Algorithms¶
Problem: A function to sort a list of numbers in ascending order
Input: nums: A list of numbers e.g. [4, 2, 6, 3, 4, 6, 2, 1]
Output: sorted_nums: The sorted version of nums e.g. [1, 2, 2, 3, 4, 4, 6, 6]
# Some test inputs & outputs
# List of numbers in random order
test0 = {
'input': {
'nums': [5, 2, 6, 1, 23, 7, -12, 12, -243, 0]
},
'output': [-243, -12, 0, 1, 2, 5, 6, 7, 12, 23]
}
# A list that's already sorted
test1 = {
'input': {
'nums': [3, 5, 6, 8, 9, 10, 99]
},
'output': [3, 5, 6, 8, 9, 10, 99]
}
# A list containing repeating elements
test2 = {
'input': {
'nums': [5, -12, 2, 6, 1, 23, 7, 7, -12, 6, 12, 1, -243, 1, 0]
},
'output': [-243, -12, -12, 0, 1, 1, 1, 2, 5, 6, 6, 7, 7, 12, 23]
}
# An empty list
test3 = {
'input': {
'nums': []
},
'output': []
}
# A very long list
import random
in_list = list(range(10000))
out_list = list(range(10000))
random.shuffle(in_list)
test4 = {
'input': {
'nums': in_list
},
'output': out_list
}
tests = [test0, test1, test2, test3, test4]
3.1 Bubble Sort 冒泡排序法¶
依次比较相邻两个elements的大小,小的在前大的在后,循环n-1次:

def bubble_sort(nums):
sorted_nums = list(nums)
if len(sorted_nums) < 2:
return sorted_nums
for _ in range(len(sorted_nums)-1):
for i in range(len(sorted_nums)-1):
if sorted_nums[i+1] < sorted_nums[i]:
sorted_nums[i], sorted_nums[i+1] = sorted_nums[i+1], sorted_nums[i]
return sorted_nums
from jovian.pythondsa import evaluate_test_cases
results = evaluate_test_cases(bubble_sort, tests)
TEST CASE #0
Input:
{'nums': [5, 2, 6, 1, 23, 7, -12, 12, -243, 0]}
Expected Output:
[-243, -12, 0, 1, 2, 5, 6, 7, 12, 23]
Actual Output:
[-243, -12, 0, 1, 2, 5, 6, 7, 12, 23]
Execution Time:
0.04 ms
Test Result:
PASSED
TEST CASE #1
Input:
{'nums': [3, 5, 6, 8, 9, 10, 99]}
Expected Output:
[3, 5, 6, 8, 9, 10, 99]
Actual Output:
[3, 5, 6, 8, 9, 10, 99]
Execution Time:
0.016 ms
Test Result:
PASSED
TEST CASE #2
Input:
{'nums': [5, -12, 2, 6, 1, 23, 7, 7, -12, 6, 12, 1, -243, 1, 0]}
Expected Output:
[-243, -12, -12, 0, 1, 1, 1, 2, 5, 6, 6, 7, 7, 12, 23]
Actual Output:
[-243, -12, -12, 0, 1, 1, 1, 2, 5, 6, 6, 7, 7, 12, 23]
Execution Time:
0.104 ms
Test Result:
PASSED
TEST CASE #3
Input:
{'nums': []}
Expected Output:
[]
Actual Output:
[]
Execution Time:
0.003 ms
Test Result:
PASSED
TEST CASE #4
Input:
{'nums': [4759, 9503, 8767, 681, 8992, 1045, 4407, 2690, 2580, 390, 9901, 7202, 7440, 7825, 8773, 88...
Expected Output:
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 2...
Actual Output:
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 2...
Execution Time:
11157.987 ms
Test Result:
PASSED
SUMMARY
TOTAL: 5, PASSED: 5, FAILED: 0
We can see that the last test cases took about 12 seconds to sort, which is too slow for us.
Time complexity: \(O(N^2)\)
Space complexity: \(O(N)\),, even thought it requires only constant/zero additional space, because the space required to store the inputs is also considered while calculating space complexity.
3.2 Insertion Sort 插入排序法¶
从前至后,将每一个元素插入至第一个小于/大于自己的元素之前
def insertion_sort(nums):
sorted_nums = list(nums)
for i in range(len(sorted_nums)):
cur = sorted_nums.pop(i) # return i position element and remove it from the list
# j = i-1
# while j >= 0 and cur < sorted_nums[j]:
# j -= 1
# sorted_nums.insert(j+1, cur)
j = 0
while j <= i-1 and cur > sorted_nums[j]:
j += 1
sorted_nums.insert(j, cur)
return sorted_nums
results = evaluate_test_cases(insertion_sort, tests)
TEST CASE #0
Input:
{'nums': [5, 2, 6, 1, 23, 7, -12, 12, -243, 0]}
Expected Output:
[-243, -12, 0, 1, 2, 5, 6, 7, 12, 23]
Actual Output:
[-243, -12, 0, 1, 2, 5, 6, 7, 12, 23]
Execution Time:
0.024 ms
Test Result:
PASSED
TEST CASE #1
Input:
{'nums': [3, 5, 6, 8, 9, 10, 99]}
Expected Output:
[3, 5, 6, 8, 9, 10, 99]
Actual Output:
[3, 5, 6, 8, 9, 10, 99]
Execution Time:
0.015 ms
Test Result:
PASSED
TEST CASE #2
Input:
{'nums': [5, -12, 2, 6, 1, 23, 7, 7, -12, 6, 12, 1, -243, 1, 0]}
Expected Output:
[-243, -12, -12, 0, 1, 1, 1, 2, 5, 6, 6, 7, 7, 12, 23]
Actual Output:
[-243, -12, -12, 0, 1, 1, 1, 2, 5, 6, 6, 7, 7, 12, 23]
Execution Time:
0.025 ms
Test Result:
PASSED
TEST CASE #3
Input:
{'nums': []}
Expected Output:
[]
Actual Output:
[]
Execution Time:
0.005 ms
Test Result:
PASSED
TEST CASE #4
Input:
{'nums': [4759, 9503, 8767, 681, 8992, 1045, 4407, 2690, 2580, 390, 9901, 7202, 7440, 7825, 8773, 88...
Expected Output:
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 2...
Actual Output:
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 2...
Execution Time:
2449.649 ms
Test Result:
PASSED
SUMMARY
TOTAL: 5, PASSED: 5, FAILED: 0
Time complexity: \(O(N^2)\)
Space complexity: \(O(1)\)
3.3 Merge Sort with Divide and Conquer(分治法)¶
3.3.1 Divide and Conquer¶
Divide the inputs into two roughly equal parts.
Recursively solve the problem individually for each of the two parts.
Combine the results to solve the problem for the original inputs.
Include terminating conditions for small or indivisible inputs.
3.3.2 Merge Sort¶
Following a visual representation of the divide and conquer applied for sorting numbers. This algorithm is known as merge sort:

def merge(nums1, nums2):
merge_nums = []
i, j = 0, 0
while i < len(nums1) and j < len(nums2):
if nums1[i] <= nums2[j]:
merge_nums.append(nums1[i])
i += 1
else:
merge_nums.append(nums2[j])
j += 1
nums1_tail, nums2_tail = nums1[i:], nums2[j:]
return merge_nums+nums1_tail+nums2_tail
def merge_sort(nums):
if len(nums) <= 1:
return nums
mid = len(nums)//2
left_nums = nums[:mid]
right_nums = nums[mid:]
left_sorted, right_sorted = merge_sort(left_nums), merge_sort(right_nums)
sorted_nums = merge(left_sorted, right_sorted)
return sorted_nums
results = evaluate_test_cases(merge_sort, tests)
TEST CASE #0
Input:
{'nums': [5, 2, 6, 1, 23, 7, -12, 12, -243, 0]}
Expected Output:
[-243, -12, 0, 1, 2, 5, 6, 7, 12, 23]
Actual Output:
[-243, -12, 0, 1, 2, 5, 6, 7, 12, 23]
Execution Time:
0.069 ms
Test Result:
PASSED
TEST CASE #1
Input:
{'nums': [3, 5, 6, 8, 9, 10, 99]}
Expected Output:
[3, 5, 6, 8, 9, 10, 99]
Actual Output:
[3, 5, 6, 8, 9, 10, 99]
Execution Time:
0.032 ms
Test Result:
PASSED
TEST CASE #2
Input:
{'nums': [5, -12, 2, 6, 1, 23, 7, 7, -12, 6, 12, 1, -243, 1, 0]}
Expected Output:
[-243, -12, -12, 0, 1, 1, 1, 2, 5, 6, 6, 7, 7, 12, 23]
Actual Output:
[-243, -12, -12, 0, 1, 1, 1, 2, 5, 6, 6, 7, 7, 12, 23]
Execution Time:
0.088 ms
Test Result:
PASSED
TEST CASE #3
Input:
{'nums': []}
Expected Output:
[]
Actual Output:
[]
Execution Time:
0.003 ms
Test Result:
PASSED
TEST CASE #4
Input:
{'nums': [4759, 9503, 8767, 681, 8992, 1045, 4407, 2690, 2580, 390, 9901, 7202, 7440, 7825, 8773, 88...
Expected Output:
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 2...
Actual Output:
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 2...
Execution Time:
65.883 ms
Test Result:
PASSED
SUMMARY
TOTAL: 5, PASSED: 5, FAILED: 0
Time complexity
For themergefunction, the time complexity is \(O(N)\), and thus we can have the time complexity ofmerge_sort:
To find the overall complexity ofmerge_sort, we simply need to count how many times themergefunction was invoked and the size of the input list for each invocation. Here’s how all the subproblems can be visualized:

Counting from the top and starting from 0, the \(k^{th}\) level of the above tree involves \(2^k\) invocations ofmergewith sublists of size roughly \(n / 2^k\), where \(n\) is the size of the original input list. Therefore the total number of comparisons at each level of the tree is \(2^k * n/2^k = n\).
Thus, if the height of the tree is \(h\), the total number of comparisons is \(n*h\). Since there are \(n\) sublists of size 1 at the lowest level, it follows that \(2^{(h-1)} = n\) i.e. \(h = \log n + 1\). Thus the time complexity of the merge sort algorithms is \(O(n \log n)\).Space complexity
To find the space complexity of merge sort, it helps to recall that a new list with equal to the sum of the sizes of the two lists is created in each invocation ofmerge.
i, j, merged = 0, 0, []
while i < len(nums1) and j < len(nums2):
if nums1[i] <= nums2[j]:
merged.append(nums1[i])
i += 1
else:
merged.append(nums2[j])
j += 1
At first glance, it may seem that \(O(n)\) space is required for each level of the tree, so the space complexity of merge sort is \(O(n \log n)\).

However, since the original sublists can be discarded after the merge operation, the additional space can be freed or reused for future merge calls. Thus, merge sort requires \(O(n)\) additional space i.e. the space complexity is \(O(n)\).
3.4 QuickSort¶
To overcome the space inefficiencies of merge sort, we’ll study another divide-and-conquer based sorting algorithm called quicksort, which works as follows:
If the list is empty or has just one element, return it. It’s already sorted.
Pick a random element from the list. This element is called a pivot.
Reorder the list so that all elements with values less than or equal to the pivot come before the pivot, while all elements with values greater than the pivot come after it. This operation is called partitioning.
The pivot element divides the array into two parts which can be sorted independently by making a recursive call to quicksort.

The key observation here is that after the partition, the pivot element is at its right place in the sorted array, and the two parts of the array can be sorted independently in-place.

def partition(nums, start=0, end=None):
if end is None:
end = len(nums)-1
l,r = start, end-1
while l < r:
if nums[l] <= nums[end]:
l += 1
elif nums[r] > nums[end]:
r -= 1
else:
nums[l], nums[r] = nums[r], nums[l]
if nums[l] > nums[end]:
nums[l], nums[end] = nums[end], nums[l]
return l
else:
return end
def quicksort(nums, start=0, end=None):
if end is None:
nums = list(nums)
end = len(nums)-1
if start < end:
pivot = partition(nums, start, end)
quicksort(nums, start, pivot-1)
quicksort(nums, pivot+1, end)
return nums
results = evaluate_test_cases(quicksort, tests)
TEST CASE #0
Input:
{'nums': [5, 2, 6, 1, 23, 7, -12, 12, -243, 0]}
Expected Output:
[-243, -12, 0, 1, 2, 5, 6, 7, 12, 23]
Actual Output:
[-243, -12, 0, 1, 2, 5, 6, 7, 12, 23]
Execution Time:
0.047 ms
Test Result:
PASSED
TEST CASE #1
Input:
{'nums': [3, 5, 6, 8, 9, 10, 99]}
Expected Output:
[3, 5, 6, 8, 9, 10, 99]
Actual Output:
[3, 5, 6, 8, 9, 10, 99]
Execution Time:
0.023 ms
Test Result:
PASSED
TEST CASE #2
Input:
{'nums': [5, -12, 2, 6, 1, 23, 7, 7, -12, 6, 12, 1, -243, 1, 0]}
Expected Output:
[-243, -12, -12, 0, 1, 1, 1, 2, 5, 6, 6, 7, 7, 12, 23]
Actual Output:
[-243, -12, -12, 0, 1, 1, 1, 2, 5, 6, 6, 7, 7, 12, 23]
Execution Time:
0.08 ms
Test Result:
PASSED
TEST CASE #3
Input:
{'nums': []}
Expected Output:
[]
Actual Output:
[]
Execution Time:
0.004 ms
Test Result:
PASSED
TEST CASE #4
Input:
{'nums': [4759, 9503, 8767, 681, 8992, 1045, 4407, 2690, 2580, 390, 9901, 7202, 7440, 7825, 8773, 88...
Expected Output:
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 2...
Actual Output:
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 2...
Execution Time:
43.799 ms
Test Result:
PASSED
SUMMARY
TOTAL: 5, PASSED: 5, FAILED: 0
Time complexity:
Best case partitioning:

If we partition the list into two nearly equal parts, then the complexity analysis is similar to that of merge sort and quicksort has the complexity \(O(n \log n)\). This is called the average-case complexity.Worst case partitioning:
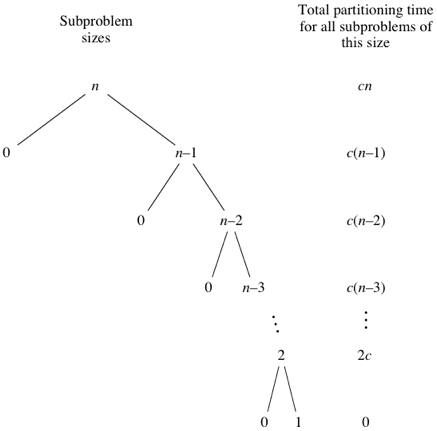
In this case, the partition is calledntimes with lists of sizesn,n-1… so that total comparisions are \(n + (n-1) + (n-2) + ... + 2 + 1 = n * (n-1) / 2\). So the worst-case complexity of quicksort is \(O(n^2)\).
Space complexity: requires \(O(1)\) additional space.
Despite the quadratic worst case time complexity Quicksort is preferred in many situations because its running time is closer to \(O(n \log n)\) in practice, especially with a good strategy for picking a pivot. Some these are:
3.5 Custom Comparison Functions¶
QUESTION: You’re working on a new feature on Jovian called “Top Notebooks of the Week”. Write a function to sort a list of notebooks in decreasing order of likes. Keep in mind that up to millions of notebooks can be created every week, so your function needs to be as efficient as possible.
class Notebook:
def __init__(self, title, username, likes):
self.title, self.username, self.likes = title, username, likes
def __repr__(self):
return 'Notebook <"{}/{}", {} likes>'.format(self.username, self.title, self.likes)
nb0 = Notebook('pytorch-basics', 'aakashns', 373)
nb1 = Notebook('linear-regression', 'siddhant', 532)
nb2 = Notebook('logistic-regression', 'vikas', 31)
nb3 = Notebook('feedforward-nn', 'sonaksh', 94)
nb4 = Notebook('cifar10-cnn', 'biraj', 2)
nb5 = Notebook('cifar10-resnet', 'tanya', 29)
nb6 = Notebook('anime-gans', 'hemanth', 80)
nb7 = Notebook('python-fundamentals', 'vishal', 136)
nb8 = Notebook('python-functions', 'aakashns', 74)
nb9 = Notebook('python-numpy', 'siddhant', 92)
notebooks = [nb0, nb1, nb2, nb3, nb4, nb5,nb6, nb7, nb8, nb9]
def compare_likes(nb1, nb2):
if nb1.likes < nb2.likes:
return "less"
elif nb1.likes == nb2.likes:
return "equal"
else:
return "more"
def merge_sort(notebooks, compare):
if len(notebooks) < 2:
return notebooks
mid = len(notebooks)//2
left, right = merge_sort(notebooks[:mid], compare), merge_sort(notebooks[mid:], compare)
return merge(left, right, compare)
def merge(left, right, compare):
merges = []
i, j = 0, 0
while i < len(left) and j < len(right):
result = compare(left[i], right[j])
if result == 'more':
merges.append(left[i])
i += 1
else:
merges.append(right[j])
j += 1
left_tail, right_tail = left[i:], right[j:]
return merges+left_tail+right_tail
sorted_notebooks = merge_sort(notebooks, compare_likes)
sorted_notebooks
[Notebook <"siddhant/linear-regression", 532 likes>,
Notebook <"aakashns/pytorch-basics", 373 likes>,
Notebook <"vishal/python-fundamentals", 136 likes>,
Notebook <"sonaksh/feedforward-nn", 94 likes>,
Notebook <"siddhant/python-numpy", 92 likes>,
Notebook <"hemanth/anime-gans", 80 likes>,
Notebook <"aakashns/python-functions", 74 likes>,
Notebook <"vikas/logistic-regression", 31 likes>,
Notebook <"tanya/cifar10-resnet", 29 likes>,
Notebook <"biraj/cifar10-cnn", 2 likes>]

